Access to technology and foundational math proficiency among students: empirical evidence from India

On this part, we first report the outcomes for the potential affect of entry to laptops by TFLS on the foundational math expertise of scholars. That is then adopted by an evaluation of heterogeneous impacts of the coverage throughout the size of wealth standing and gender. We then carry out quite a lot of robustness checks to make sure that our double distinction identification design is selecting up the impact of the coverage and never producing a spurious outcome.

Most important findings

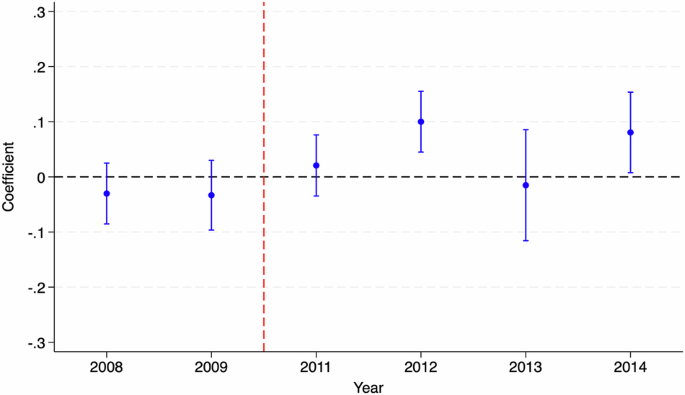
We report the outcomes from our double distinction identification design in Desk 3. The outcomes recommend that the potential publicity to the TFLS program had a optimistic impact on the foundational math proficiency of scholars. We, particularly, observe that the mathematics scores are round 0.085 factors greater for college students who have been probably uncovered to this system. This interprets to an impact dimension of two.3% when in comparison with the imply. The outcome implies that entry to laptops can probably assist in bettering fundamental foundational math expertise of upper secondary college students. We additionally observe within the dynamic double distinction graph in Fig. 1 that our outcomes are pushed by enchancment in foundational math proficiency of scholars within the years 2012 and 2014. This is smart because the implementation of the TFLS program solely started in September 2011. We additionally observe negligible results for the 12 months 2013, which could probably be on account of the differential distribution cycle for the laptop computer program in several years.

We additional assess the degrees at which these studying enhancements occur for arithmetic when college students get entry to laptops. For this function, we estimate a linear likelihood mannequin the place our dependent variable now turns into a dummy which takes the worth 1 if the scholar has achieved talent atleast at a sure stage of studying in arithmetic (Chakraborty and Jayaraman, 2019; Chatterjee and Poddar, 2021; Lahoti and Sahoo, 2020). This various formulation additionally has the benefit of addressing the problem of ordinality of math proficiency scores, which we use for our main evaluation. It’s because the variable capturing proficiency scores is steady in nature and may, due to this fact, be affected by the selection of scale. Utilizing a linear likelihood mannequin helps us to account for this concern as properly.

Desk 4 reviews the outcomes for this train to grasp the degrees of studying. We observe that the affect of entry to laptops is far greater for greater ranges of studying, reminiscent of subtraction and division, when in comparison with decrease ranges of studying. College students who have been probably uncovered to this system have been 5% (when in comparison with the imply) extra prone to be proficient in subtraction when in comparison with college students who weren’t uncovered to this system. Whereas the coefficient for division is imprecisely estimated, we nonetheless discover that uncovered college students have been 4.6% extra prone to be proficient in it when in comparison with college students not uncovered to the coverage. We don’t discover enchancment in decrease ranges of studying, because the coefficients are a lot nearer to zero.

Sub-sample evaluation and heterogeneity

The training literature from India means that academic inequalities persist within the nation by way of gender, caste, faith, and financial standing (Asadullah and Yalonetzky, 2012; Borooah, 2012; Desai and Kulkarni, 2008; Gandhi Kingdon, 2002; Kingdon, 2007; Varughese and Bairagya, 2020). Therefore, it’s doable that the heterogeneous results of the Tamil Nadu Free Laptop computer program on math expertise could exist based mostly on beneficiary college students’ particular person attributes in addition to social and non secular affiliation. Sadly, our information doesn’t present us with info on the caste and faith of the scholar. Within the subsequent subsections, we due to this fact concentrate on the financial standing in addition to the gender of the scholar to grasp potential impacts of the coverage based mostly on these attributes.

Financial standing

Our lowered kind evaluation means that entry to technological assets reminiscent of laptops might help to enhance the mathematics expertise of scholars. As these assets are much less reasonably priced for college students coming from resource-constrained households, the availability of free laptops to college students from these backgrounds can have a lot bigger impacts when in comparison with college students coming from economically better-off households that may have already got entry to those assets. Nevertheless, additionally it is doable that poor households receiving laptops contemplate it as a one-off financial alternative to learn from the sale of the asset. On this case, laptops may have a lot smaller, if any, impacts on college students from these backgrounds.

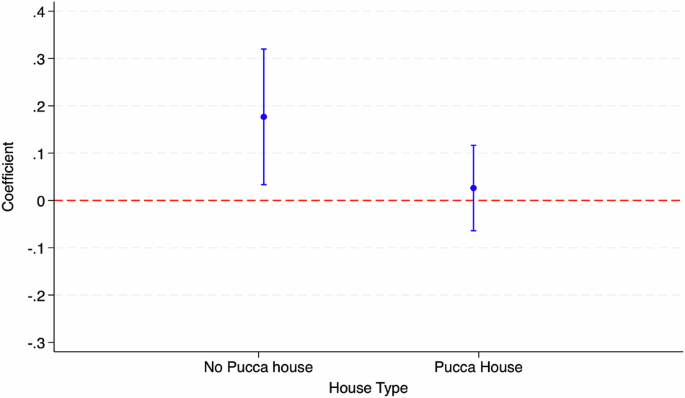
The ASER information doesn’t present us with direct info on the financial standing of the scholar. Nevertheless, current literature on India means that info on housing property serves as an excellent proxy for a similar (Chakraborty and Jayaraman, 2019). We, due to this fact, use information on housing high quality to grasp heterogeneity by the financial standing of the scholar. Right here, we concentrate on whether or not a pupil stays in a “Pucca home” or not, the place “Pucca home” refers to sturdy homes product of burnt bricks and cement. We conjecture {that a} pupil residing in a “Pucca home” is prone to be economically properly off in a relative sense when in comparison with a pupil residing in a “Kutcha or Semi-Pucca” home. Determine 2 plots the coefficients for sub-sample evaluation for 2 completely different home varieties. We discover that college students not residing in “Pucca home” and belonging to economically poorer households have been the first beneficiaries of this system by way of their studying outcomes. College students residing in “Pucca homes,” who have been additionally prone to be significantly better off economically, skilled no optimistic results of the TFLS program.

The determine reveals sub-sample estimates (together with 95% confidence interval) for math proficiency for college students residing in a “Pucca home” or “No Pucca home” utilizing ASER information.

Gender

We then look at if entry to laptops on account of the TFLS had any differential impacts on the mathematics scores of girls and boys. Present literature factors in direction of differential use of computer systems for girls and boys that may probably lead to differential results (Fairlie, 2016; Fairlie and Robinson, 2013). Additionally, within the Indian setting, the place ladies proceed to expertise academic drawback in class classroom settings, extra centered and customized entry to assets by laptops has the potential to offer bigger payoffs (Adukia, 2017; Chatterjee and Poddar, 2021; Gandhi Kingdon, 2002; Kingdon, 2007). Moreover, if ladies begin from a decrease base in math expertise when in comparison with boys, the marginal impacts of entry to laptops could be a lot greater for them. Quite the opposite, if boys begin from a decrease base, the marginal impacts for them are prone to be greater when in comparison with ladies (Contini et al., 2017; Fryer and Levitt, 2010; Welmond and Gregory, 2021). The literature additionally means that in a resource-constrained setting, girls and ladies is likely to be much less prone to retain management over technological property reminiscent of mobiles and laptops, because the management would possibly move on to a male relative or the asset is likely to be offered off (Roessler et al., 2021). If that occurs, improved entry to laptops by TFLS will lead to a lot decrease common optimistic affect on the mathematics expertise of ladies when in comparison with boys.

We, due to this fact, carry out a sub-sample evaluation for the potential affect of this system on the mathematics expertise of girls and boys in Desk 5. As we will observe from the sub-sample evaluation in Column (1) and Column (2), the mathematics expertise of each girls and boys seemingly improved on account of the TFLS. Nevertheless, the coefficient for boys is nearly double when in comparison with that of the women. After we examine additional, we discover that this distinction in coefficient is certainly pushed by economically constrained households not residing in “pucca homes” (Desk 6). Therefore, it’s doable that differential selling-off of laptops offered to women by economically constrained households can probably be one of many causes for decrease results skilled by them. This additionally is smart contemplating that anecdotal proof on the coverage from media reviews means that a number of laptops distributed below the scheme do seem on the gray market; nevertheless, we shouldn’t have sufficient info on whether or not this was extra outstanding for lady beneficiaries.^{Footnote 21,Footnote 22}

One other potential issue that might have led to decrease marginal optimistic results on math scores for ladies when in comparison with boys could also be their greater beginning base stage within the topic. Whereas proof on the international stage means that ladies lag behind boys in math outcomes, proof opposite to the identical can also be current for some international locations and contexts.^{Footnote 23} (Contini et al., 2017; Fryer and Levitt, 2010; Welmond and Gregory, 2021). Within the case of India, proof signifies a gender hole in arithmetic for predominantly North Indian States and, in distinction, a “reverse” gender hole the place boys lag behind ladies in predominantly South Indian states, together with Tamil Nadu (Das and Singhal, 2023). Das and Singhal (2023) additionally depend on the ASER dataset for his or her evaluation, as is the case on this research. After we have a look at our information, we discover that boys (pre-policy imply math rating = 3.790) learning at school twelfth of presidency colleges in Tamil Nadu lag behind in arithmetic when in comparison with ladies (pre-policy imply math rating = 3.835) in the identical cohort. Therefore, greater optimistic impacts of the Tamil Nadu Free Laptop computer program for boys can even probably replicate boys catching up with ladies by way of math scores, as they begin from a decrease base.

Robustness checks

Cohort falsification

Our double distinction identification technique depends on the usage of cohort variation to select the results of the TFLS program. Basically, we’re evaluating the foundational math proficiency of scholars at school twelfth (eligible cohort) with these at school eleventh (ineligible cohort) and saying that within the absence of this system, the distinction between the outcomes of those two cohorts can be zero. To check the validity of this identification assumption, we conduct a falsification examine by evaluating the outcomes of sophistication eleventh with these of sophistication tenth college students utilizing the regression specification offered in Equation (1). Right here, we offer a faokaye treatment to class eleventh college students and evaluate their outcomes to class tenth college students. To do that, we generate a dummy variable “Class 11” which takes the worth 1 if the scholar is in Class 11 of the federal government faculty and nil if pupil is in Class 10 of the federal government faculty. Since each these cohorts have been basically ineligible for this system, ideally, we must always not discover their foundational math expertise to be statistically completely different from one another.

We report the outcomes for this managed experiment in Desk 7 (Duflo, 2001). As anticipated, we don’t discover any statistical distinction between the mathematics studying outcomes of sophistication eleventh and sophistication tenth college students in Tamil Nadu. This provides us confidence that our double distinction identification design is selecting up the true causal impact of the TFLS program.

Various management group

We additionally attempt to take a look at the sensitivity of our estimates to various definitions of the management group, i.e., the ineligible cohort. To do that, we now pool class 10 college students and sophistication 11 college students collectively as a mixed management group, i.e., the ineligible cohort, and evaluate their outcomes with the eligible handled group, i.e., class 12 college students, earlier than and after this system implementation in Tamil Nadu. The outcomes for this train are reported in Desk 8. As we will observe, the coefficients from the train are similar to our principal estimates, thereby offering us confidence that our identification technique is appropriately selecting up the impact of this system.

Choice into authorities colleges

A possible concern for our evaluation is that if this system altered the enrollment in authorities vis-a-vis personal colleges. That is doable as college students would possibly swap from personal to authorities colleges to achieve entry to program advantages. This has the potential to introduce choice bias in our outcomes, as inclusion in our pattern is conditional on a pupil learning in a authorities faculty. We, due to this fact, take a look at if the introduction of this system impacted the chance of people enrolling in authorities vis-a-vis personal colleges and current our leads to Desk 9. The outcomes recommend that this system didn’t have any affect on the chance of scholars enrolling in a authorities faculty when put next with a personal faculty.

Various technique: triple distinction

On this part, we devise another triple distinction technique to check the robustness of our outcomes estimated utilizing a double distinction design (Gruber, 1994). Right here, we introduce a 3rd dimension to our current double distinction framework within the type of a state variation. Because of this we now evaluate the foundational math proficiency of our eligible cohort (class twelfth) to that of the ineligible cohort (class eleventh) throughout our handled state of Tamil Nadu and different management states in India, earlier than and after this system.^{Footnote 24,Footnote 25} Apart from informing in regards to the sensitivity of our principal estimates, an extra benefit of utilizing this various technique is that it permits us to discover potential channels, utilizing each ASER and IHDS datasets, by which the TFLS could affect foundational math expertise. It’s because it will increase the statistical energy and the precision with which we will choose the results on account of a bigger pattern dimension accorded by the technique. As an illustration, the information on English language competency that we discover as a possible channel is simply accessible within the years 2009, 2012, and 2014. Equally, the state-level pattern in IHDS is sort of small from the attitude of performing intra-state cohort-level evaluation utilizing a difference-in-difference design. The utilization of the triple distinction design right here helps us to extend the precision with which we will pick the results of the TFLS on these intermediate variables that function potential channels for our results.

In an effort to carry out a triple distinction evaluation, we run the regression equation given beneath for every pupil i belonging to family h from village v in state s. As earlier than, we limit our evaluation to college students learning in authorities colleges, because the scheme was solely accessible to them.

In Equation (2), α_s and δ_t seize state fastened results and time fastened results, respectively. Treated is a dummy variable that takes the worth 1 for the handled state of Tamil Nadu and nil, in any other case. Eligible and Post discuss with dummies for the eligible cohort and post-policy interval, respectively. Right here, θ₁ is our coefficient of curiosity that picks out the impact of the TFLS program on the foundational math proficiency of scholars. We additionally use strong customary errors clustered on the state stage for our evaluation right here.

Utilizing Desk 10 and Fig. 3, we first present that the parallel tendencies assumption for the triple distinction mannequin is happy (Muralidharan and Prakash, 2017). We then current the outcomes from our triple distinction design in Desk 11. As could be noticed, the outcomes look similar to our main estimates utilizing a double distinction design. This provides us confidence that our main technique, based mostly on a double distinction design, is appropriately selecting the impacts of TFLS. As acknowledged earlier than, we use this triple distinction design to check potential channels for our results on foundational math proficiency within the subsequent part.

The determine reveals dynamic triple distinction estimates (together with 95% confidence interval) for Math Proficiency utilizing ASER information. The 12 months 2010 has been thought-about as the bottom 12 months for the plot.

Different issues and checks

A possible concern with our evaluation is that the ASER information solely covers college students as much as the age of 16 years to gather info on foundational math proficiency. Whereas college students aged 16 years have been eligible to be enrolled at school twelfth and constituted a major proportion of enrolled college students within the grade each in 2012 and earlier years in Tamil Nadu (NUEPA, 2013a, 2013b), this creates a priority in that we’re lacking out on college students from higher age cohorts, e.g., 17–18 years of age, who may need additionally been enrolled at school twelfth and could also be characteristically completely different from college students aged 16 years.^{Footnote 26} Nevertheless, literature on the affect of age on studying outcomes means that this relationship is prone to be robust solely within the early grades (Deming and Dynarski, 2008). Contemplating that we’re taking a look at an end result that’s a lot beneath the grade stage, the affect of the age of scholars learning at school twelfth on our estimates is prone to be minimal. We additional run a mannequin, the place we management for age fastened results to account for time-invariant traits associated to age. The outcomes for this train are reported in Desk 12 and are consistent with our principal estimates. We additionally conduct one other examine the place we report estimates from a special specification the place we cluster the usual errors on the district stage and report the leads to Desk 13. As we will observe, the outcomes are similar to our principal estimates and are strong to the usage of bootstrap p values.